策略梯度方法推导

轨迹$\tau = (s_{0},a_{0},…,s_{h},a_{h})$

目标：找到最优神经网络参数$\theta^{*}$最大化收益关于轨迹分布的期望

$\theta^{*}=\mathop{\arg\max}\limits_{\theta} \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\bigg[\sum\limits_{t}r(s_{t},a_{t})\bigg]$

目标函数 $J(\theta)=\mathbb{E}_{\tau\sim p_{\theta}(\tau)}\bigg[\sum\limits_{t}r(s_t,a_t)\bigg]$

定义轨迹收益$r(\tau)=\sum\limits_t r(s_t,a_t)$，目标函数变成$J(\theta)=\mathbb{E}_{\tau\sim p_{\theta}(\tau)}[r(\tau)]$

假设$\tau$的分布函数$p_{\theta}(\tau)$是可微的，拆开期望： $J(\theta)=\int p_{\theta}(\tau)r(\tau)\,{\rm d}\tau$

对两边求梯度：$\nabla_{\theta} J(\theta)=\int \nabla_{\theta} p_{\theta}(\tau)r(\tau)\,{\rm d}\tau$

其中等式$\nabla_{\theta}p_{\theta}(\tau) = p_{\theta}(\tau)\nabla_\theta logp_\theta(\tau)$成立

因此

$\begin{align} \nabla_{\theta} J(\theta)&=\int p_{\theta}(\tau)\nabla_\theta logp_\theta(\tau)r(\tau)\,{\rm d}\tau\\ &= \mathbb{E}_{\tau\sim p_\theta(\tau)}\bigg[\nabla_\theta logp_\theta(\tau)r(\tau)\bigg]\end{align}$

其中$p_{\theta}(\tau)=p(s_1)\prod\limits_{t=1}^{T}\pi_{\theta}(a_t,s_t)p(s_{t+1})$

则$\nabla_\theta logp_\theta(\tau) = \nabla_\theta \sum \limits_{t=1}^{T}log\pi_{\theta}(a_t,s_t)$

$\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau\sim p_\theta(\tau)}\bigg[\bigg( \sum \limits_{t=1}^{T}\nabla_\theta log\pi_{\theta}(a_t,s_t)\bigg)\bigg(\sum \limits_{t=1}^{T}r(s_t,a_t)\bigg)\bigg]$

实际抽样时用平均来进行估算

$\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum \limits_{i=1}^{N} \bigg[\bigg( \sum \limits_{t=1}^{T}\nabla_\theta log\pi_{\theta}(a_{i,t},s_{i,t})\bigg)\bigg(\sum \limits_{t=1}^{T}r(s_{i,t},a_{i,t})\bigg)\bigg]$

之后用 $\theta \gets \theta + \nabla_{\theta} J(\theta)$更新参数$\theta$

解决高方差问题

改变因果关系

当前时间策略只能影响之后的奖励

$\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum \limits_{i=1}^{N}\sum \limits_{t=1}^{T} \bigg[\bigg( \nabla_\theta log\pi_{\theta}(a_{i,t},s_{i,t})\bigg)\bigg(\sum \limits_{t’=t}^{T}r(s_{i,t’},a_{i,t’})\bigg)\bigg]$

引入基线

$\nabla_{\theta} J(\theta)= \mathbb{E}_{\tau\sim p_\theta(\tau)}\bigg[\nabla_\theta logp_\theta(\tau)(r(\tau)-b)\bigg]$

eg： $b_t = \frac{1}{N} \sum \limits_{i} Q^\pi(s_{i,t},a_{i,t})$

解决样本效率问题

问题：每次更新参数$\theta$ 都要重新进行采样，数据利用率低，会影响到收敛的速度 怎么利用之前的样本？

重要性采样

原理：

$\mathbb{E}_{x \sim p(x)}[f(x)] = \int p(x)f(x)\, {\rm d}x = \int q(x)\frac{p(x)}{q(x)}f(x)\,{\rm d}x = \mathbb{E}_{x \sim q(x)}[\frac{p(x)}{q(x)}f(x)] $

从q(x)中采样来替代从p(x)中采样

修改：

应用到目标函数

$ J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[r(\tau)] = \mathbb{E}_{\tau \sim p_{\theta^{old}}(\tau)}\bigg[\frac{p_{\theta}(\tau)}{p_{\theta^{old}}(\tau)}\bigg]$

比值项

$\frac{p_{\theta}(\tau)}{p_{\theta^{old}}(\tau)} = \frac{p(s_{1})\prod \limits_{t=1}^{T}\pi_{\theta}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t})}{p(s_{1})\prod \limits_{t=1}^{T}\pi_{\theta^{old}}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t})} = \frac{\prod \limits_{t=1}^{T}\pi_{\theta}(a_{t}|s_{t})}{\prod \limits_{t=1}^{T}\pi_{\theta^{old}}(a_{t}|s_{t})}$

得出

$\nabla_{\theta}J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\bigg[\sum \limits_{t=1}^{T} \nabla_{\theta} log \pi_{\theta}(a_t|s_t)\bigg(\prod \limits_{t’=1}^{t} \frac{\pi_{\theta}(a_{t’}|s_{t’})}{\pi_{\theta^{old}}(a_{t’}|s_{t’})}\bigg)\bigg(\sum \limits_{t’ =t}^{T}r(s_{t’},a_{t’})-b\bigg)\bigg]$

连乘可能趋于0’

修改

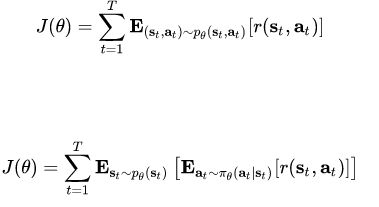
最终

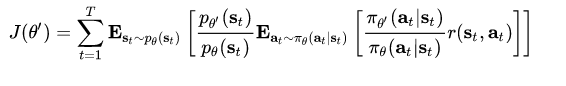
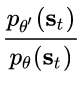
近似1

可以拿出去加基线

新参数可以利用旧采样，一段时间后再重新采样？