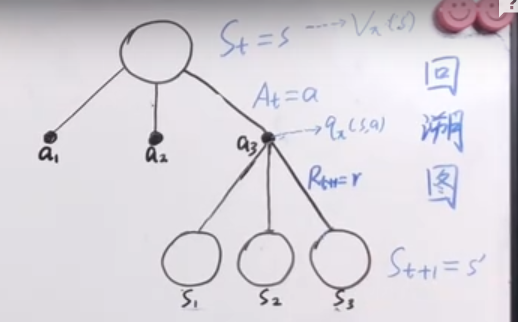
TRPO
重要性采样
原理:
$\mathbb{E}_{x \sim p(x)}[f(x)] = \int p(x)f(x)\, {\rm d}x = \int q(x)\frac{p(x)}{q(x)}f(x)\,{\rm d}x = \mathbb{E}_{x \sim q(x)}[\frac{p(x)}{q(x)}f(x)] $
从q(x)中采样来替代从p(x)中采样
修改:
应用到目标函数
$ J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[r(\tau)] = \mathbb{E}_{\tau \sim p_{\theta^{old}}(\tau)}\bigg[\frac{p_{\theta}(\tau)}{p_{\theta^{old}}(\tau) }r(\tau)\bigg]$
比值项
$\frac{p_{\theta}(\tau)}{p_{\theta^{old}}(\tau)} = \frac{p(s_{1})\prod \limits_{t=1}^{T}\pi_{\theta}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t})}{p(s_{1})\prod \limits_{t=1}^{T}\pi_{\theta^{old}}(a_{t}|s_{t})p(s_{t+1}|s_{t},a_{t})} = \frac{\prod \limits_{t=1}^{T}\pi_{\theta}(a_{t}|s_{t})}{\prod \limits_{t=1}^{T}\pi_{\theta^{old}}(a_{t}|s_{t})}$
得出
$\nabla_{\theta}J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}\bigg[\sum \limits_{t=1}^{T} \nabla_{\theta} log \pi_{\theta}(a_t|s_t)\bigg(\prod \limits_{t’=1}^{t} \frac{\pi_{\theta}(a_{t’}|s_{t’})}{\pi_{\theta^{old}}(a_{t’}|s_{t’})}\bigg)\bigg(\sum \limits_{t’ =t}^{T}r(s_{t’},a_{t’})-b\bigg)\bigg]$
MM
Majorize-Minimization 最小化上界函数
Minorize-Maximization 最大化下界函数
Surrogate function
原目标函数非凸,很难优化,求解逼近于目标函数的替代函数,不断迭代替代函数。
目标函数:策略的期望折扣奖励
替代函数:是目标函数的下界函数,可用于估计当前策略的期望奖励,易于优化
TRPO
策略梯度中,参数的更新为$\theta_{new} = \theta_{old}+\alpha \nabla_{\theta}J$
这种方法对于步长$\alpha$的选取很难控制,如果步长不合适,可能会导致目标函数反而越来越差。
目标: 找到一个合适的步长,使每次更新时目标函数都单调递增。
方法:希望目标函数(期望回报函数)单调递增,那么可以将新策略的期望回报函数分解成原有策略回报函数加一个永远为正的项。
得到等式
$\eta(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{\tau \in \tilde{\pi}}\bigg[\sum \limits^{\infty}_{t=0}A_\pi(s_t,a_t)\bigg]$
其中
$A_\pi(s,a)=Q_\pi(s,a) - V_\pi(s)=\mathbb{E}_{s’\sim P(s’|s,a)}[r(s)+\gamma V^\pi(s’)-V^\pi(s)]$
其中r(s) 即为R(s,a,s’)
公式证明:
将公式写开得到:
$\eta(\tilde{\pi})=\eta(\pi)+\sum \limits^{\infty}_{t=0} \sum \limits_{s}P(s_t = s|\tilde{\pi})\sum \limits_{a}\tilde{\pi}(a|s)\gamma^tA_\pi(s,a)$
进一步变形:
$\eta(\tilde{\pi})=\eta(\pi)+ \sum \limits_{s}\rho_{\tilde{\pi}}(s)\sum \limits_{a}\tilde{\pi}(a|s)\gamma^tA_\pi(s,a)$
$\rho_\pi(s)=P(s_0=s)+\gamma P(s_1=s)+\gamma^2P(s_2=s)+…+\gamma^t(s_t=s)$
其中$\rho_{\tilde{\pi}}(s)$是新策略下的动态特性,但新策略此时还未知,且旧策略与新策略之间改动不大,因此用旧策略$\rho_{\pi}(s)$代替新策略。
在动作分布上利用重要性采样
$\sum \limits_{a} \tilde{\pi}_{\theta}(a|s_n)A_{\theta_{old}}(s_n,a)=\mathbb{E}_{a \sim q_{old}}\bigg[\frac{\tilde\pi_\theta(a|s_n) }{\pi_{\theta_{old}}(a|s_n) }A_{\theta_{old}(s_n,a)}\bigg]$
q为旧参数下的动作分布
记
$L_\pi(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{s \sim \rho_{\theta_{old}},a \sim \pi_{\theta_{old}}}\bigg[\frac{\tilde\pi_\theta(a|s_n) }{\pi_{\theta_{old}}(a|s_n) }A_{\theta_{old}(s_n,a)}\bigg]$
引入不等式来取目标回报函数的下界,之后最大化下界
$\eta(\tilde \pi) \ge L_\pi(\tilde \pi) - CD^{max}_{KL}(\pi,\tilde \pi)$
其中$C = \frac {4 \in \gamma}{(1-\gamma)^2}$
$D^{max}_{KL}(\pi,\tilde \pi)$为固定状态下动作分布kl散度的最大值
但很难在每个策略下找到KL散度的最大值,因此使用KL散度的均值
$\bar{D}^{\rho_{\theta_{old}}}_{KL}(\pi,\tilde \pi) = \mathbb{E}_{s \sim \rho}[D_{KL}(\pi(\cdot|s)||\tilde\pi(\cdot|s))]$
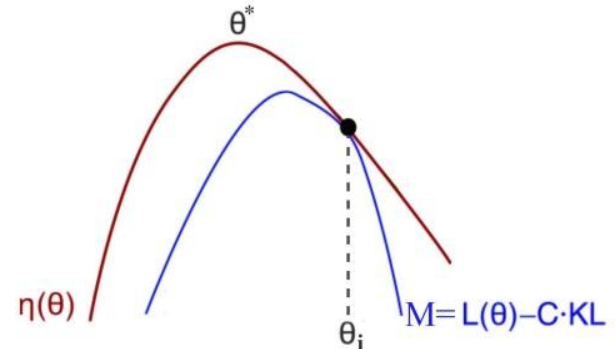
记$M_i(\pi) = L_{\pi_i}(\tilde \pi)-C\bar{D}^{\rho_{\theta_{old}}}_{KL}(\pi,\tilde \pi)$
容易得到 $\eta(\pi_{i+1}) \ge M_i(\pi_{i+1})$且$\eta(\pi_i)=M_i(\pi_i)$
则 $\eta(\pi_{i+1})-\eta(\pi_{i}) \ge M_i(\pi_{i+1})-M_i(\pi_{i})$
那么,寻找使Mi最大的策略即可以保证策略的期望回报单调递增,那么寻找策略的过程就是一个不断寻找Mi最大值的过程
$\max \limits_{\theta}[L_{\theta_{old}}-C\bar{D}^{\rho_{\theta_{old}}}_{KL}(\theta_{old},\theta)]$
最终得到
为了使问题更加可解,将问题等效为
$\max \limits_{\theta}\mathbb{E}_{s \sim \rho_{\theta_{old}},a \sim \pi_{\theta_{old}}}\bigg[\frac{\tilde\pi_\theta(a|s_n) }{\pi_{\theta_{old}}(a|s_n) }A_{\theta_{old}(s_n,a)}\bigg]$ 满足约束$\bar{D}^{\rho_{\theta_{old}}}_{KL}(\theta_{old},\theta) \le \eta$
理解
在不断更新$\theta$的同时,替代函数也在不断逼近目标函数,最终会达到一个局部最优解
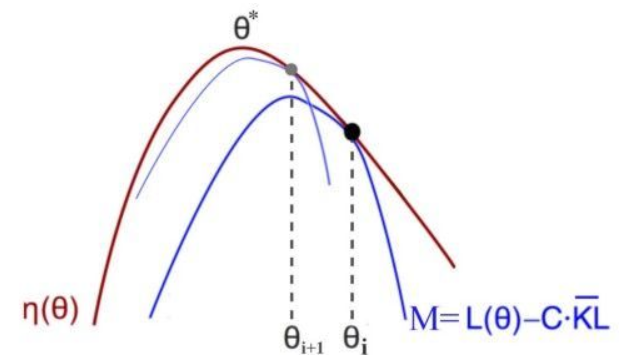
迭代更新过程
参考博客:
https://blog.csdn.net/tanjia6999/article/details/99716133
https://blog.csdn.net/weixin_41679411/article/details/82421121